


The slow convergence in bisection method is due to the fact that the absolute error is halved at each step. For this, f(a) and f(b) should be of opposite nature i.e. Note: Bisection method guarantees the convergence of a function f(x) if it is continuous on the interval (denoted by x1 and x2 in the above algorithm. The algorithm and flowchart presented above can be used to understand how bisection method works and to write program for bisection method in any programming language. *Now the loop continues with new values.* If (f1*f2) > 0, then display initial guesses are wrong and goto (11).Find root of function in interval a, b (Or find a value of x such that f (x) is 0).
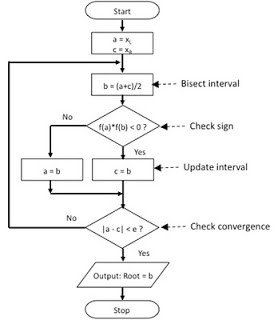
Here f (x) represents algebraic or transcendental equation. It never fails! The overall accuracy obtained is very good, so it is more reliable in comparison to the Regula-Falsi method or the Newton-Raphson method.Į is the absolute error i.e. Given a function f (x) on floating number x and two numbers ‘a’ and ‘b’ such that f (a)f (b) < 0 and f (x) is continuous in a, b. It is the simplest method with slow but steady rate of convergence. In this C program, x0 & x1 are two initial guesses, e is tolerable error and f (x) is actual function whose root is being obtained using bisection method. In this post, the algorithm and flowchart for bisection method has been presented along with its salient features.īisection method is a closed bracket method and requires two initial guesses. This program implements Bisection Method for finding real root of nonlinear equation in C programming language. According to the theorem “If a function f(x)=0 is continuous in an interval (a,b), such that f(a) and f(b) are of opposite nature or opposite signs, then there exists at least one or an odd number of roots between a and b.” The process is based on the ‘ Intermediate Value Theorem‘. Bisection method is used to find the real roots of a nonlinear equation.


 0 kommentar(er)
0 kommentar(er)
